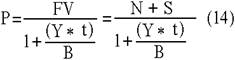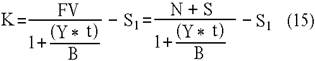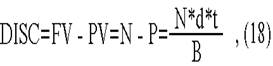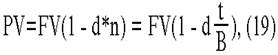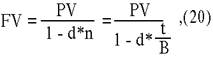Поскольку номинал дисконтного векселя принимается за 100%, его курсовая стоимость равна:

где – t число дней до погашения.

При Y=r рыночная стоимость обязательства на момент выпуска будет равна номиналу (т.е. Р=N). Соответственно, при Y>r будет Р<N и вексель размещается с дисконтом, а в случае Y<r с премией (т.е. Р>N).

Таким образом, рыночная стоимость векселя с учетом накопленного дохода, определяемая из (14), может отклоняться от номинала. Однако в биржевой практике принято котировать в процентах к номиналу, т.е. за 100 единиц на дату сделки. При этом ставка дохода по обязательствам r показывается отдельно.

где t - число дней до погашения;

S1 – абсолютная величина дохода, накопленная к дате совершения сделки.

где t1 - число дней от момента выпуска до даты сделки.

Таким образом, полная рыночная стоимость векселя Р может быть так же определена как:

P = K + S1

Анализ учета векселей.

При учете вексель выполняет две функции: коммерческого кредита и средства платежа.

Абсолютная величина дисконта определяется как разность между номиналом векселя и его современной стоимостью на момент проведения

операции. При этом дисконтирование осуществляется по учетной ставке d, устанавливаемой банком:

где t - число дней до погашения;

d - учетная ставка банка;

P - сумма, уплаченная владельцу при учете векселя;

N - номинал;

Суть данного метода заключается в том, что проценты начисляются на сумму, подлежащую уплате в конце срока операции. При этом применяется учетная ставка d.

При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 360/365(366). Используемую при этом норму приведения называют антисипативной ставкой процентов[1].

Учетная ставка d иногда применяется и для наращивания по простым процентам. Необходимость в таком наращивании возникает при определении будущей суммы контракта, например, общей суммы векселя. Формула определения будущей величины в этом случае имеет вид:

Простой вексель на сумму 100 000 с оплатой через 90 дней учитывается в банке за 60 дней до погашения. Учетная ставка банка 15 %. Определить величину дисконта в пользу банка и сумму, полученную владельцем векселя.

Disc = (100000 * 60 * 0.15) / 360 = 2500;

Соответственно, владелец векселя получит величину PV:

PV=100000 – 2500 = 97500;

Предположим, что в рассматриваемом примере владелец векселя решил учесть вексель немедленно после получения, тогда:

Disc = (100000 * 90 * 0.15) / 360 = 3750;

PV = 100000 – 3750 = 96250;

Как следует из полученного результата, при неизменном значении ставки d чем раньше производится учет векселя, тем больше будет величина дисконта в пользу банка и тем меньшую сумму получит владелец. Изменим условия примера 1 следующим образом.